목차
이상치 탐지는 비지도 학습에 해당하며 보통과 많이 다른 샘플을 감지하는 것을 의미한다.
그렇다면, PCA를 사용하여 Kaggle에 있는 신용카드 데이터셋의 이상 거래를 예측해보면서 PCA를 활용한 이상치 탐지에 대한 아이디어를 이해해보자.
https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud
Credit Card Fraud Detection
Anonymized credit card transactions labeled as fraudulent or genuine
www.kaggle.com
1. Data Load, Data Understanding
# 1. Data Load
data = pd.read_csv('../data/creditcard.csv')
data.head()
# 2. Class의 뷸균형
data.describe()
# 3. Class의 개수
data['Class'].value_counts()
이 데이터셋은 2013년 9월 2일간의 신용 카드 거래에 대한 데이터들로 구성되어 있다. Feature V1...V28은 보안 상의 문제로 인해 PCA로 만든 Feature이며 Time은 각 트랜잭션 사이의 경과된 초를 의미하고 Amount는 거래 금액을 의미한다. 또한, 이 데이터셋에 타겟 변수(예측 변수)인 Class는 0(정상 거래)과 1(사기 거래)로 구성되어 있다.

describe 함수의 결과를 보면 (V1...V28은 해석할 수 없으므로 캡쳐할 때 잘라냈다.) Amount 컬럼의 min, max 값의 편차가 심한 것을 알 수 있고, Class 컬럼은 0과 1로 구성된 범주형 변수이지만 평균값이 약 0.001로 불균형이 심한 데이터셋임을 알 수 있다.

Class 컬럼에 value_counts()을 적용한 결과 284807개의 데이터 중 오직 492개만 사기 거래임을 알 수 있다. 때문에, Kaggle에서는 이러한 데이터 불균형에 대해 "Confusion Matrix를 통한 정확도는 의미가 없고 AUPRC(Area Under the Precision-Recall Curve)를 사용하여 정확도를 측정하는 것이 좋다"라고 설명을 하고 있다. 그렇다면, 왜 정확도는 의미가 없고 PR Curve가 의미가 있는지에 대해 알아보자.
Q1. 왜 PR Curve로 정확도를 측정해야 하는 가?
먼저, 지도학습 모델인 Logistic Regression을 학습하여 정확도를 측정해보겠다.
# X, y로 분리
data_X = data.copy().drop('Class', axis=1)
data_y = data['Class'].copy()
# Scaling
from sklearn.preprocessing import StandardScaler
s_scaler = StandardScaler() # mean 값을 뺀 것으로 마이너스 값이 존재한다.
data_X.loc[:,:] = s_scaler.fit_transform(data_X) # 모든 행과 열에 대해서 스케일링을 함
# train set, test set split
X_train, X_test, y_train, y_test = train_test_split(data_X, data_y, test_size=0.33,
random_state=2018, stratify=data_y)
# 데이터셋 비율 확인
X_train.shape, X_test.shape, y_train.shape, y_test.shape
# ((190820, 30), (93987, 30), (190820,), (93987,))
y_train.mean(), y_test.mean()
# (0.0017293784718582959, 0.0017236426314277506)
먼저, X, y로 데이터를 나누고 Standard Scaler를 통해 Scaling을 진행한다. Min-Max Scaler가 아닌 Standard Scaler를 사용하는 이유는 Amount 컬럼에서 max값이 매우 크기 때문에(이상치) 이상치에 민감한 Standard Scaler를 사용해 각 Feature들을 표준화 시켜주는 것이다.
Min-Max Scaler는 데이터에서 가장 작은 값을 0으로 가장 큰 값을 1로 두고 0과 1 사이로 정규화 시키는 것이기 때문에 이상치로 인해 값의 분포가 이상해질 수 있는 반면, Standard Scaler는 특성들의 평균을 0으로 분산을 1로 표준화 하는 것(각 컬럼을 평균으로 빼서 표준편차로 나눠줌)으로 해당 데이터셋에 적합함
다음은 학습을 위해 train set과 test set으로 나누었는데, 이때 stratify 파라미터를 사용하여 데이터의 비율을 맞춰주었다. Class 컬럼의 1의 개수만 현저히 적은 데이터 불균형이 있어서 그냥 무작위로 데이터셋을 나눈다면 데이터셋의 크기가 큰 train으로 1이 다 들어갈 수 있는 위험성이 있기 때문이다. 그래서 stratify를 data_y(원본 데이터의 class컬럼)로 비율을 맞춰준 것이다. (shape, mean으로 비율이 맞춰진 것을 알 수 있다.)
# LogisticRegression
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
logreg = LogisticRegression()
logreg.fit(X_train, y_train) # 학습
y_pred = logreg.predict(X_test)
print(classification_report(y_test, y_pred))
Logistic Regression으로 학습시켜 classification_report를 생성한 결과 정확도(accuracy)가 무려 1이 나오는 것을 알 수 있다. 분명 1(사기거래)를 정확하게 예측하지 못했지만 데이터의 불균형으로 정확도가 1이 나온 것이다. 때문에, Precision과 Recall과 같은 평가 지표를 보고 해석 해야 한다는 것이다. 그렇다면 Precision-Recall Curve와 Average Precision을 한번 구해보자.
Precision은 모델이 Positive라고 예측한 것 중에서 실제로 Positive한 비율이고 Recall은 실제로 Positive에서 모델이 Positive라고 예측한 비율을 뜻한다. 이 모델에서는 Class 1에 대한 Precision은 0.85이고 Recall 0.69이기 때문에 실제 Class가 1(사기 거래)이지만 모델이 알맞게 사기 거래라고 예측한 비율이 69% 밖에 되지 않는 것이다.
# 1. precision_recall_curve
precision, recall, thresholds = precision_recall_curve(y_test, logreg.predict_proba(X_test)[:,1])
plt.plot(recall, precision, label='precision-recall curve (Logistic Regression)')
plt.legend()
plt.xlabel('Recall')
plt.ylabel('Precision')
# 2. Average Precision
average_precision_score(y_test, logreg.predict_proba(X_test)[:,1])
# 0.7709756449173383
Precision-Recall Curve(PR Curve)는 파라미터인 Threshold를 변화시키면서 Precision과 Recall을 구한 그래프이고 Average Precision(AP)는 PR Curve의 선 아래 면적으로 계산되며 1에 가까울 수록 모델이 우수하다는 것을 의미한다. 그러므로, Logistic Regression 모델은 77% 정도의 성능이라고 이해하면 된다.
2. PCA로 이상치탐지하기
다시 본론으로 돌아와 PCA로 이상치를 탐지해보자.
우선, 이상치탐지(Anomaly Detection)는 보통과 많이 다른 샘플을 감지하는 작업이다. 이 데이터셋에서는 보통(정상거래, 0)과 다른 이상치(사기거래, 1)를 탐지한다고 예를 들 수 있다. 정상과 이상에 대한 라벨이 없을 때 (or 라벨을 만들기 어려울 때)나 위의 설명에서 Logistic Regression을 사용하여 학습한 결과 데이터의 불균형으로 인해 정확도는 1이 나오는 문제와 같이 지도학습 알고리즘을 적용하기 어려울 때에 그 대안으로 비지도학습 이상 탐지 기법을 사용하여 정상과 이상에 대한 라벨링을 할 수 있다. (데이터에 이상치가 매우 적게 나타날 때 유용한 기법이다)
비지도학습 이상 탐지 기법 중 하나인 PCA(Principal Component Analysis)는 가장 대표적인 차원 축소 알고리즘이다. 차원 축소를 하면 정보 손실이 일어나기 때문에 축소했던 것을 다시 원래대로 재구성하면 원본과 똑같지 않고 어느정도의 차이가 생겨나게 된다. 이 차이를 이용하여 보통 샘플의 재구성 오차보다 이상치의 재구성 오차가 훨씬 크다는 것을 이용해 이상치를 판별할 수 있다.
Q2. 이상치의 재구성 오차가 크다?

위의 그림에서 왼쪽은 원본 그림이고 오른쪽은 PCA를 적용했다가 재구성했을 때의 그림이다. 정보 손실이 일어났지만 어느 정도는 원본과 비슷한 것을 알 수 있다. 여기에서 차원 축소를 하게 되면 데이터들이 공통으로 많이 갖게 되는 정보만 남게 된다는 것을 느낄 수 있는데, 이상치들은 공통으로 갖고있는 정보가 거의 없기 때문에 정보 손실이 많이 일어나게 되고 재구성 시에 그 오차가 훨씬 커지게 되는 것이다.
때문에, PCA 적용 시에 원래 feature의 수와 주성분의 개수를 같게 한다면 이상치의 정보들을 포함하기 때문에 재구성하더라도 그 오차가 크지않아 정상과 이상치를 분류하기 어려워지는 것을 직접 볼 수가 있다! 그렇다면, 해당 데이터셋으로 원래 feature의 수인 30과 그 수보다 작은 27개의 주성분으로 구성하는 PCA 모델을 각각 만들어보고 그 성능을 비교해보자.
2-1. Anomaly Score 계산 함수 생성
먼저, 재구성 오차를 계산하는 함수를 만들어보자. 이렇게 원본 데이터와 재구성된 데이터 사이의 평균 제곱 거리를 재구성 오차라고 한다. 다음 코드는 원래의 df(original_df)와 재구성된 df(reduced_df)를 넣으면 재구성 오차를 구하는 코드이다.
def anomaly_score(original_df, reduced_df):
loss = np.sum((np.array(original_df) - np.array(reduced_df)) ** 2, axis=1)
loss = pd.Series(loss)
loss = (loss - np.min(loss)) / (np.max(loss) - np.min(loss))
return loss
2-2. PCA, n_components = 30
다음 코드는 PCA의 주성분의 개수를 30으로 설정하여 train set으로 학습 시킨 뒤 적용하고 (fit_transform) test set에도 적용(transform)하여 anomaly_proba를 구하는 코드이다.
# PCA 적용
from sklearn.decomposition import PCA
n_components = 30
pca = PCA(n_components=n_components, random_state=2018)
X_train_PCA = pca.fit_transform(X_train)
X_test_PCA = pca.transform(X_test)
X_test_PCA_inverse = pca.inverse_transform(X_test_PCA)
anomaly_proba = anomaly_score(X_test, X_test_PCA_inverse)
# 1. PR Curve
plt.figure(figsize=(3,3))
precision, recall, thresholds = precision_recall_curve(y_test, anomaly_proba)
plt.title('precision-recall curve (PCA(n=27)) on Train Set')
plt.plot(recall, precision)
plt.xlabel('Recall')
plt.ylabel('Precision')
# 2. Average Precision Score
average_precision_score(y_test, anomaly_proba)
# 0.16569554776441534
2-2. PCA, n_components = 27
다음 코드는 PCA의 주성분의 개수를 27로 설정하여 train set으로 학습 시킨 뒤 적용하고 (fit_transform) test set에도 적용(transform)하여 anomaly_proba를 구하는 코드이다.
# PCA 적용
from sklearn.decomposition import PCA
n_components = 27
pca = PCA(n_components=n_components, random_state=2018)
X_train_PCA = pca.fit_transform(X_train)
X_test_PCA = pca.transform(X_test)
X_test_PCA_inverse = pca.inverse_transform(X_test_PCA)
anomaly_proba = anomaly_score(X_test, X_test_PCA_inverse)
# 1. PR Curve
plt.figure(figsize=(3,3))
precision, recall, thresholds = precision_recall_curve(y_test, anomaly_proba)
plt.title('precision-recall curve (PCA(n=27)) on Train Set')
plt.plot(recall, precision)
plt.xlabel('Recall')
plt.ylabel('Precision')
# 2. Average Precision Score
# average_precision_score(y_test, anomaly_proba)
# 0.698094725274565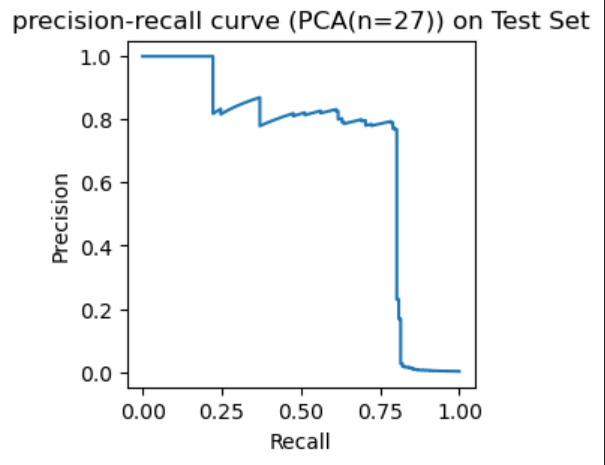
두 모델을 비교해보면 주성분 30개의 PCA 모델은 AP Score가 약 0.16이고 주성분 27개의 PCA 모델의 AP Score는 약 0.69로 차원을 축소했을 때 이상치를 잘 분류했다는 것을 알 수 있다. 이렇게 보통 샘플의 재구성 오차와 이상치의 재구성 오차를 비교해 후자가 더 크다는 것을 이용하여 PCA를 통해 간단하고 효과적인 이상치 탐지를 할 수 있다.
'Python > 머신러닝-딥러닝' 카테고리의 다른 글
| (머신러닝)타이타닉 데이터 셋으로 보는 Classification(분류)_4. 나이브 베이즈 (0) | 2023.06.06 |
|---|---|
| (머신러닝)타이타닉 데이터 셋으로 보는 Classification(분류)_3. KNN (K-최근접 이웃) (0) | 2023.06.06 |
| (머신러닝)타이타닉 데이터 셋으로 보는 Classification(분류)_2. 로지스틱 회귀(Logistic Regression) (0) | 2023.06.06 |
| (머신러닝)타이타닉 데이터 셋으로 보는 Classification(분류)_1. Rule Based (0) | 2023.06.06 |





댓글